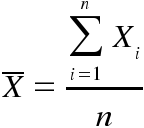Nessa primeira etapa básica sobre estatística aprendemos a calcular médias: aritimética, geométrica, harmônica. Vimos o que é moda e mediana, como achá-las. Além de estudarmos também as medidas de dispersão: variância, desvio-padrão, coeficiente de variação... e outras coisas mais.
Cada ser humano tem um jeito melhor para aprender e fixar os conteúdos vistos, deixo aqui minha dica:
EXERCITEM, quanto mais exercício melhor, principalmente com os números. A matemática é maliciosa e quando pensamos que sabemos de tudo ainda não sabemos de nada.
Segue um site com assuntos e exercícios para você praticar:
http://www.somatematica.com.br/estat/basica/exercicios.php
Este é um blog que foi criado afim de ajudar os estudantes de Administração e os curiosos sobre o assunto: Estatística. Caso nosso blog atendeu suas expectativas, dê o seu voto. ;)
segunda-feira, 10 de outubro de 2011
terça-feira, 27 de setembro de 2011
Medidas de Variação ou Dispersão
∿∿∿∿∿∿∿∿∿∿∿∿∿∿∿∿ ┥Variação
Variação ↥ ↧ Qualidade
Corresponde ao estudo da oscilação (variação) de cada elemento em relação a sua medida.
*Instrumentos
➜ Variância : amostral / populacional
➜ Desvio-Padrão : amostral / populacional
Variação ↥ ↧ Qualidade
Corresponde ao estudo da oscilação (variação) de cada elemento em relação a sua medida.
*Instrumentos
➜ Variância : amostral / populacional
segunda-feira, 5 de setembro de 2011
Frequência
Frequência Absoluta (fi ):
Def: é o número de vezes que o valor de determinada variável é observado.
Def: é a soma das frequências absolutas anteriores com a frequência absoluta deste valor.
Def: é o quociente entre a frequência absoluta do valor da variável e o número total de observações.
Def: é a soma das frequências relativas anteriores com a frequência relativa desse valor.
Mediana e moda
Mediana
Def: quer dizer o valor do meio, ou seja, se temos: X={1,2,3}, a mediana será 2 e se for Y={1,2,3,4}, a mediana será 2,5.
Para chegarmos nestas conclusões temos as seguintes fórmulas:
Amostra ímpar:
X= (n+1)/2
Com esta fórmula acharemos a posição da mediana.
EX:
X={2,5,6,8,9}
X=5+1/2 = 3, ou seja, o 3º elemento que é 6.
Amostra par:
X=[(n/2)+(n/2)+1]/2
Esta nos indica os elementos, assim substituímos tais elementos e dividimos por dois.
EX:
X={3,5,7,9}
X=[(4/2)+(4/2)+1]/2 = 2+3/2 =
=2º + 3º (elementos)/2 = 5+7/2 = 6.
Moda
Def: significa ser o valor que mais se repete no conjunto.
EX1:
X={1,1,2,3,4,5,6}
Moda = 1.
Neste caso, como só existe uma única moda, ele é uni modal ou modal.
EX2:
X={1,1,2,4,5,6,8,2}
Moda = 1 e 2.
Neste caso, como existem duas modas, ele é bimodal.
EX3:
X={1,1,3,3,4,5,6,7,1,2,3,4,4}
Moda = 1,3 e 4.
Neste caso, como existe mais de duas modas, ele é multimodal ou plurimodal.
EX4:
X={3,4,3,4}
Moda = ∉.
Neste caso, como NÃO existe moda, ele é amodal.
OBS: Sempre que for resolver problemas com medidas da estatística (MÉDIAS, MEDIANA E MODA), têm que colocar os algarismos em ordem crescente.
terça-feira, 30 de agosto de 2011
Média Aritmética, Geométrica e Harmônica.
Média Aritmética
É o tipo de média mais utilizada pelas pessoas no dia-a-dia e subdivide-se em dois tipos: simples e ponderada. A diferença entre elas é que na média aritmética a importância (peso) de cada ocorrência é igual e na ponderada cada termo possui uma importância relativa, ou seja, possuem pesos diferentes.
A fórmula genérica da média aritmética simples é:
Ela é obtida dividindo-se as somas das observações pela quantidade das mesmas.
Exemplos:
Um aluno tirou as seguintes notas na disciplina de matemática: 6,2,7,9. Qual a média?
x= 6+2+7+9 / 4
x= 6
Exemplo 2: Calcular a média aritmética de: 9, 13 e 20
x= 9+13+20 /3
x= 14
A média aritmética ponderada possui a seguinte fórmula:

Ela é obtida através da soma dos produtos de cada um multiplicado por seus respectivos pesos e dividida pela soma dos pesos.
Exemplo:
Pedro participou de um concurso onde foi realizada provas de Português, Matemática, Biologia e História. Essas provas tinham peso 3,3,2 e 2, respectivamente. Pedro tirou 8.0 em português, 7.5 em matemática, 5.0 em biologia e 4.0 em história. Qual a média que ele obteve?
Média Geométrica
Esse tipo de média tem várias aplicações. É muito utilizada na área de finanças e de engenharia. Lembrando que a média geométrica de um conjunto é sempre menor ou igual a média aritmética, vários problemas de desigualdades como na geometria são resolvidos através dela.
A média geométrica de um conjunto de números positivos é definida como o produto de todos os membros do conjunto elevado ao inverso do número de membros
Este tipo de média é calculada multiplicando-se todos os valores e extraindo-se a raiz de índice n deste produto.
A fórmula desse tipo de média é:
Supomos então, que temos os números 4, 6 e 9 e multiplicamos os elementos e obtemos o produto 216. Pegamos então este produto e extraímos a sua raiz cúbica, chegando ao valor médio 6.
Extraímos a raiz cúbica, pois o conjunto é composto de 3 elementos. Se fossem n elementos, extrairíamos a raiz de índice n.
Exemplo: A média geométrica entre 1,2 e 4.
Uma outra utilização para este tipo de média,é com variações percentuais em sequência. Como por exemplo:
Digamos que uma categoria de operários tenha um aumento salarial de 20% após um mês, 12% após dois meses e 7% após três meses. Qual o percentual médio mensal de aumento desta categoria?
Média Harmônica
A média harmônica dos números reais positivos é definida como sendo o número de membros dividido pela soma dos inverso dos membros.
Esse tipo de média nunca é maior que a média aritmética ou a geométrica. Ela é utilizada quando se trata de grandezas inversamente proporcionais.


É o tipo de média mais utilizada pelas pessoas no dia-a-dia e subdivide-se em dois tipos: simples e ponderada. A diferença entre elas é que na média aritmética a importância (peso) de cada ocorrência é igual e na ponderada cada termo possui uma importância relativa, ou seja, possuem pesos diferentes.
A fórmula genérica da média aritmética simples é:
Ela é obtida dividindo-se as somas das observações pela quantidade das mesmas.
Exemplos:
Um aluno tirou as seguintes notas na disciplina de matemática: 6,2,7,9. Qual a média?
x= 6+2+7+9 / 4
x= 6
Exemplo 2: Calcular a média aritmética de: 9, 13 e 20
x= 9+13+20 /3
x= 14
A média aritmética ponderada possui a seguinte fórmula:

Ela é obtida através da soma dos produtos de cada um multiplicado por seus respectivos pesos e dividida pela soma dos pesos.
Exemplo:
Pedro participou de um concurso onde foi realizada provas de Português, Matemática, Biologia e História. Essas provas tinham peso 3,3,2 e 2, respectivamente. Pedro tirou 8.0 em português, 7.5 em matemática, 5.0 em biologia e 4.0 em história. Qual a média que ele obteve?
Média Geométrica
Esse tipo de média tem várias aplicações. É muito utilizada na área de finanças e de engenharia. Lembrando que a média geométrica de um conjunto é sempre menor ou igual a média aritmética, vários problemas de desigualdades como na geometria são resolvidos através dela.
A média geométrica de um conjunto de números positivos é definida como o produto de todos os membros do conjunto elevado ao inverso do número de membros
Este tipo de média é calculada multiplicando-se todos os valores e extraindo-se a raiz de índice n deste produto.
A fórmula desse tipo de média é:
Supomos então, que temos os números 4, 6 e 9 e multiplicamos os elementos e obtemos o produto 216. Pegamos então este produto e extraímos a sua raiz cúbica, chegando ao valor médio 6.
Extraímos a raiz cúbica, pois o conjunto é composto de 3 elementos. Se fossem n elementos, extrairíamos a raiz de índice n.
Exemplo: A média geométrica entre 1,2 e 4.
Uma outra utilização para este tipo de média,é com variações percentuais em sequência. Como por exemplo:
Digamos que uma categoria de operários tenha um aumento salarial de 20% após um mês, 12% após dois meses e 7% após três meses. Qual o percentual médio mensal de aumento desta categoria?
Média Harmônica
A média harmônica dos números reais positivos é definida como sendo o número de membros dividido pela soma dos inverso dos membros.
Esse tipo de média nunca é maior que a média aritmética ou a geométrica. Ela é utilizada quando se trata de grandezas inversamente proporcionais.

Exemplo 1: Média harmônica de 2, 6 e 8.

Exemplo 2: Suponha que em uma determinada viagem, um carro desenvolva duas velocidades distintas, durante a metade do percurso ele manteve a velocidade de 50 km/h e durante a metade restante sua velocidade foi de 60 km/h. Vamos determinar a velocidade média do veículo no percurso.
Exemplo 3: Média harmônica entre 1,2,3 e 4.
quinta-feira, 18 de agosto de 2011
Resumo inicial sobre Estatística
Antes de iniciar as medidas da estatística, iremos ver a simbologia da mesma.
∑ = símbolo de somatório;
n = Número de elementos;
i = índice de soma, ou seja, é de onde você irá iniciar sua “contagem”.
Para explicar melhor vamos dar uma olhada em uma parte do site: www.atractor.pt/mat/sem_palavras/saber_mais/somatorio.htm
O somatório
A adição é uma das operações básicas da aritmética. O símbolo usual para esta operação é o sinal mais ("+") e cada um dos termos a somar designa-se por parcelas. Assim, por exemplo, a soma de 1, 2 e 4 é denotada por:
1 + 2 + 4.
Em muitas situações o número de parcelas a somar é muito grande e não é viável denotar a adição desta forma. Uma possível solução consiste em esconder as parcelas intermédias atrás de reticências ("..."), deixando claro o modo como se podem reconstituir essas parcelas. Assim, a soma de todos os números naturais de 1 a 1000 pode ser indicada por:
1 + 2 + 3 + 4 + … + 1000 (*).
Esta forma muitas vezes não é a melhor uma vez que apenas temos acesso às parcelas omitidas de forma implícita, o que pode originar algumas ambiguidades. De modo alternativo, uma soma pode ser representada abreviadamente pelo símbolo de somatório (letra maiúscula grega Sigma)

Onde i é o chamado índice da soma, que toma valores inteiros entre N1 (limite inferior) e N2 (limite superior), e f é a função que descreve as parcelas da adição. Por exemplo, na adição (*) N1 = 1, N2 = 1000 e f é a função identidade:
O número de parcelas de uma adição representada nesta forma é igual a (N2 + 1) - N1. Mais alguns exemplos:
Com esta notação abreviada de somatório, também é possível descrever somas com um número infinito de parcelas. Para tal, basta considerar N1 = - (o símbolo
quarta-feira, 10 de agosto de 2011
Onde está a Estatística ?
Antes de dizer onde está a estatística, primeiro temos que saber o que é. Uma associação que é dada a palavra ESTATÍSTICA é a ideia de "coleção de numeros" ou seja da organização e da apresentação de contagens e medições. No entanto, a Estatística não deve ser vista como simples "coleção de numeros" porque estes não são coletados para serem armazenados, eles servem para tomadas de decisões .
Encontramos a Estatística aqui no Brasil nos assuntos mais diversos como taxas de natalidade e valores de taxas de câmbio. Por exemplo, é com base em indices de audiência, que uma emissora de televisão pode tirar um programa do ar ou modificar o final previsto de uma novela, é com base em pesquisa de opinião que um candidato a cargo eletivo pode modificar certas atitudes, é com base na quantidade vendida de um produto em determinado periodo que um supermercado pode aumentar ou diminuir o estoque desse produto.
Pequena introdução sobre a nossa querida estatística.
Fonte: livro - Elementos da Estatítica (Sonia Vieira) Ed.Atlas
Prof. André Xavier
Estudantes: Daniele Cunha
Duane Karla
Glaucia Raphaela
Larissa Cintia
Assinar:
Comentários (Atom)